Conceito de erro - Metrologia

Considera-se uma série de medições de uma determinada grandeza (exemplos: comprimento, temperatura, pressão, tensão elétrica, etc). Sejam os parâmetros:

X: valor verdadeiro dessa grandeza.

X_i: valor da medição de ordem i.

O erro de medição E é dado pela diferença entre os valores acima:

E = X − X_i #A.1#

Alguns aspectos sobre medições podem ser lembrados:

• Não há medição sem erro.
• A qualidade de uma medição depende da estimativa do erro.
• O erro pode ser apenas estimado, porque não há instrumento ideal (perfeitamente exato) que indique o valor verdadeiro.

Considerando a totalidade das medições, o erro pode ser dado em relação ao valor médio X:

E = X − X  #A.2#

Em qualquer caso, desde que não se conhece o valor verdadeiro, o erro pode ser apenas estimado.

Conceito de incerteza

Incerteza é geralmente definida por um parâmetro, relacionado ao resultado de uma medição, que caracteriza a dispersão de valores que pode ser atribuída a esse resultado. Em geral, é determinada com base no desvio-padrão dos valores medidos. Exemplo:

Seja o resultado da medição de um determinado comprimento dado por (20 ± 0,3) mm. A incerteza dessa medição é 0,3 mm.

Conceito de exatidão

A exatidão é definida pelo desvio máximo, em relação ao valor verdadeiro x, de uma série de medidas X_i:

max |X − X_i|  #B.1#

Portanto, a expressão os resultados da medição são exatos significa resultados próximos do valor verdadeiro.

Conceito de precisão

Precisão é uma medida da reprodutibilidade, geralmente expressa pela maior diferença entre os valores medidos e a média desses valores:

max |X_i − X|  #C.1#

Portanto, a expressão os resultados da medição são precisos significa resultados próximos entre si.

Embora sejam sinônimos na linguagem do dia-a-dia, exatidão e precisão são, conforme visto, coisas distintas no conceito técnico. A Figura 01 usa o clássico exemplo do tiro ao alvo para ilustrar graficamente a diferença. Na analogia, o centro do alvo seria o valor verdadeiro e as coordenadas dos tiros seriam as medições.

Fig 01

Em (a) os resultados são exatos porque, em média, estão próximos do valor verdadeiro, mas não são precisos porque há certa dispersão.

Em (d) os resultados são precisos porque estão próximos entre si, mas não são exatos porque estão distantes do valor verdadeiro.

Em (b) a situação ideal (precisos e exatos) e, em (c), a pior situação, isto é, nem precisos nem exatos.

Comparando (d) com a situação ideal (b), é possível concluir que o atirador deve ser habilidoso, mas a mira da arma deve estar desregulada. E, na comparação de (a) com (d), deduz-se que a mira da arma está em ordem, mas o atirador não tem a necessária habilidade.

Tipos de erros

Erros sistemáticos são parcelas de erros que tendem a se repetir nas medições. Fatores humanos são as causas mais comuns (exemplos: instrumento não calibrado, leitura em ângulo de um instrumento com escala e ponteiro, procedimento incorreto, etc). Teoricamente os erros sistemáticos podem ser antecipados, medidos ou deduzidos e os resultados podem ser corrigidos após as medições.

Erros aleatórios, como o nome indica, ocorrem ao acaso e não podem ser previstos (exemplos: falhas de contagem, ruídos em um circuito elétrico, etc). Assim, os erros aleatórios não podem ser eliminados e não há medições sem a sua presença. Mas podem ser reduzidos através da repetição das medições, uma vez que, em média, os erros aleatórios tendem a se cancelar.

Algarismos significativos

Qualquer instrumento de medição, do mais simples ao mais sofisticado, apresenta um intervalo ou resolução mínima de medição, abaixo do qual não se pode ter certeza do valor indicado.

No exemplo da Figura 01 é suposto que os intervalos representam centímetros. Assim, pode-se afirmar, com certeza, que o comprimento da barra azul é algo entre 7 e 8 cm. A fração menor que 1 cm pode apenas ser estimada com alguma dúvida. Por exemplo, 7,3 cm. Isso significa que o algarismo 3 é incerto nessa medição.

Notar que seria inadequado e incorreto escrever, por exemplo, 7,30 cm. Se a fração decimal é incerta, frações menores não têm nenhum significado.

Fig 01

Algarismos significativos são todos os que expressam o valor medido até o primeiro incerto, inclusive este último. Zeros consecutivos à esquerda não são considerados significativos. Exemplos:

• 2,01 tem 3 significativos.
• 0,00043 tem 2 significativos.
• 4500 tem 4 significativos, etc (considerando, é claro, que o último algarismo é o incerto).

Zeros à direita são considerados e não podem ser desprezados no caso de medições. Exemplo:

• 25,0 cm não é o mesmo que 25,00 cm. Este último é resultado de uma medição mais precisa, com incerteza na faixa de centésimos de cm contra décimos de cm do primeiro.

Se não especificada, é usual que a incerteza seja subentendida como uma unidade decimal da casa correspondente ao último algarismo. Exemplo:

• 24,08 mm equivale a 24,08 ± 0,01 mm.

Se a incerteza é conhecida, ela deve ser especificada. Exemplo:

• 12,26 ± 0,02 mm.

Alguns autores recomendam o uso de parênteses para indicar que os números se referem à mesma unidade. Portanto, no exemplo anterior,

• (12,26 ± 0,02) mm.

A incerteza deve estar sempre alinhada com o último algarismo. Exemplo: a notação 12,2 ± 0,03 é completamente equivocada.

Arredondamentos

Quando o número de casas decimais for maior que o necessário, ou seja, um desvio maior é aceitável, pode-se arredondar os valores com o método clássico (supondo o arredondamento da n-ésima casa decimal):

1-) Se o valor descartado é menor que 0,5 10^-n, isto é, o primeiro dígito é menor que 5, o n-ésimo decimal permanece inalterado (arredondamento para baixo).

2-) Se o valor descartado é maior que 0,5 10^-n, isto é, o primeiro dígito é maior que 5, adiciona-se 1 ao n-ésimo decimal (arredondamento para cima).

3-) Se o valor descartado é igual 0,5 10^-n, o n-ésimo decimal é o valor par mais próximo. De outra forma: adiciona-se 1 ao n-ésimo decimal se ele for ímpar ou o n-ésimo decimal permanece inalterado se ele for par.

Exemplos de arredondamento para 1,4535:

• 1,454 (3ª casa).
• 1,45 (2ª casa).
• 1,4 (1ª casa).

Observar que, se o arredondamento for executado com algarismos à esquerda da vírgula, o resultado pode entrar em conflito com o critério de algarismos significativos. Exemplo:

• 14563 pode ser arredondado para 15000, mas isso dá idéia de 5 significativos, o que não é mais verdade. Melhor escrever
• 1,4563 10⁴ e arredondar para 1,5 10⁴.

Combinação de incertezas - Introdução

Grandezas físicas podem ser medidas diretamente nos casos em que o instrumento fornece a indicação final. Exemplo: um voltímetro indica a tensão elétrica entre dois pontos. Há também, por razões técnicas ou econômicas, grandezas cujos valores são obtidos indiretamente, através da medição de outras grandezas e das relações matemáticas entre elas.

Como exemplo de medição indireta, pode-se citar a velocidade obtida a partir da relação dos valores medidos de distância e de tempo. Desde que todas as medições têm incertezas, a questão é saber, nesse caso, a incerteza para o valor calculado de velocidade a partir das incertezas obtidas das medições de distância e de tempo.

De forma genérica, pode-se dizer que há uma grandeza g dada por uma função matemática de outras x₁, x₂, etc. Ou seja,

#A.1#

É usual simbolizar a incerteza com a letra u (do inglês "uncertainty") seguida do símbolo da grandeza entre parênteses. Assim, o objetivo é a determinação, a partir da função anterior, da incerteza u(g) como uma função f_udas incertezas individuais u(x₁), u(x₂), etc:

#A.2#

Combinação de incertezas - Grandezas dependentes

Grandezas estatisticamente dependentes são, em geral, aquelas obtidas pelo mesmo instrumento. Exemplo: um paquímetro é usado para medir as arestas de um paralelepípedo e, com os valores, o seu volume é calculado.

O uso do mesmo instrumento aumenta a probabilidade da sobreposição de desvios, de forma que a incerteza combinada de grandezas dependentes é relativamente maior que a de grandezas independentes.

Considerando

#A.1#

e  x₁, x₂, etc  grandezas dependentes, a fórmula genérica é dada por:

#B.1#

A igualdade acima pode ser usada em casos particulares comuns (soma, subtração, multiplicação, etc) para obter fórmulas simples e diretas.

Antes da menção a esses casos, consideram-se as definições:

• incerteza absoluta é a incerteza em unidades físicas, u(x_i) conforme já visto. Exemplo: se o resultado de ordem i de uma medição genérica i é (20,0 ± 0,2) mm, os valores são x_i = 20,0 mm  e  u(x_i) = 0,2 mm.

• incerteza relativa é a relação entre a incerteza absoluta e o valor da grandeza:

#B.2#

Para o exemplo anterior, ela é dada por 0,2 / 20 = 0,01.

• incerteza percentual é a incerteza relativa multiplicada por 100:

#B.3#

Deve-se notar, entretanto, que nem sempre incertezas relativas e percentuais são intercambiáveis na mesma fórmula.

Os itens seguintes dão os casos particulares mais comuns para combinação de incertezas de grandezas dependentes (igualdade #B.1#).

1) Soma e subtração

#C.1#

Portanto, na soma ou na subtração, as incertezas absolutas são somadas.

2) Multiplicação por constante

#D.1#

A igualdade acima é facilmente deduzida a partir da anterior (#C.1#).

3) Multiplicação e divisão

#E.1#

#E.2#

Portanto, na multiplicação ou na divisão, as incertezas relativas são somadas.

4) Potenciação

#F.1#

A fórmula acima é conseqüência da igualdade #E.1# do item anterior.

Exemplo 01: o resultado da medição do diâmetro D de um eixo de seção circular foi 20,0 ± 0,2 mm. Determinar a área S da seção transversal desse eixo e a respectiva incerteza.

Calculando a área,

S = (π / 4) D² = (π / 4) 20² = 314,2 mm²

De acordo com #D.1#,

u(S) = u[ (π / 4) D² ] = (π / 4) u(D²)

De acordo com #F.1#,

u(D²) / D² = 2 u(D) / D.

Assim,

u(D²) = 2 u(D) D.

Substituindo na anterior,

u(S) = (π / 4) 2 u(D) D = (π / 4) 2 0,2 20 = 6,3 mm²

Portanto, o resultado da área é dado por

R(S) = (314,2 ± 6,3) mm²

O exemplo anterior mostra que, em princípio, é possível juntar igualdades do itens 1 a 4 para obter resultados. Às vezes, o uso de uma variável auxiliar pode ajudar. Seja, por exemplo,

g = x₁ / (x₂ + x₃).

Se é feito y = x₂ + x₃, ocorre g = x₁ / y.

Assim, calculam-se u(y) de acordo com #C.1# e u(g) de acordo com #E.2#. Entretanto, esse procedimento nem sempre é válido. Se, por exemplo,

g = (x₁ + x₂) / (x₁ + x₃), deve-se determinar as derivadas parciais segundo #B.1#.

Combinação de incertezas - Grandezas independentes

Medições executadas com instrumentos diferentes produzem em geral grandezas independentes. Assim, a probabilidade de sobreposição de variações numa mesma direção é presumivelmente pequena, e a incerteza resultante é menor, se comparada com a combinação de grandezas dependentes.

Considera-se a grandeza g dada pela função:

#A.1#

Onde x₁, x₂, ... são independentes.

Então, a incerteza de g é obtida pela fórmula genérica:

#B.1#

Há uma evidente semelhança com a fórmula para grandezas dependentes vista em página anterior. A diferença é o uso da soma dos quadrados no lugar da soma simples.

Os itens seguintes dão os resultados da fórmula acima para alguns casos particulares comuns.

1) Soma e subtração

#C.1#

Portanto, na soma ou na subtração, o quadrado da incerteza combinada é igual à soma dos quadrados das incertezas individuais.

2) Multiplicação e divisão

#D.1#

Portanto, na multiplicação ou na divisão de grandezas independentes, o quadrado da incerteza relativa combinada é igual à soma dos quadrados das incertezas relativas individuais.

Exemplo 01: um micrômetro foi usado para medir a largura B da seção transversal de uma barra de seção retangular, chegando-se ao resultado (25,000 ± 0,005) mm. A altura H da seção foi medida com um paquímetro, obtendo-se o resultado (100,00 ± 0,04) mm. Determinar a incerteza combinada para a área S da seção transversal da barra.

As grandezas B e H são independentes porque foram obtidas por meio de instrumentos diferentes. Desde que S = B H, usa-se a fórmula #D.1#:

[ u(S) / S ]² = [ u(B) / B ]² + [ u(H) / H ]² =

(0,005/25)² + (0,04/100)² = 2 10⁻⁷

[ u(S) / S ] = √ (2 10⁻⁷)

Calculando,

S = B H = 25 100 = 2500,0 mm²

u(S) = 2500,0 √ (2 10⁻⁷) ≈ 1,1 mm²

Exemplo 02: deseja-se determinar a massa específica ρ de um material a partir de uma amostra cilíndrica. A massa M é medida com uma balança, resultando em M ± u(M). O diâmetro e a altura (D e H) são medidos com instrumentos diferentes, resultando em D ± u(D) e H ± u(H) respectivamente. Desenvolver a fórmula para a relação entre a incerteza da massa específica u(ρ) e as incertezas dessas medições.

A função para a massa específica é facilmente dedutível:

ρ = f(M, D, H) = (4/π) M / (D² H)

As grandezas são claramente independentes e, desde que, além de multiplicação e divisão, há operação de potenciação, as fórmulas anteriores para casos particulares não podem ser usadas. Assim, é aplicada a fórmula básica #B.1#, que deve ser considerada sempre que a relação matemática não puder ser reduzida a casos simples.

Determinando as derivadas parciais,

∂ ρ / ∂ M = (4/π) / (D² H)

∂ ρ / ∂ D = (4/π) (−2) M / (D³ H)

∂ ρ / ∂ H = (4/π) (−1) M / (D² H²)

Substituindo em #B.1# e simplificando,

u(ρ)² =

(4/π)² { [u(M) / (D² H)]² + [u(D) / (−2) / (D³ H)]² + [u(H) / (−1) / (D² H²)]²

A simplificação pode ser maior se as parcelas são divididas por ρ² da relação básica anterior:

[ u(ρ) / ρ ]² = [ u(M) / M ]² + [ 2 u(D) / D ]² + [ u(H) / H ]²

Com a igualdade acima, a incerteza da massa específica u(ρ) é obtida a partir dos valores medidos, das respectivas incertezas e do valor calculado de ρ = (4/π) M / (D² H).

Combinação de incertezas - Grandezas parcialmente dependentes

Em páginas anteriores, foram examinados métodos separados para combinação de incertezas de grandezas dependentes e de grandezas independentes. Há, entretanto, casos em que ambas as situações estão presentes. Exemplo: o volume de um paralelepípedo é calculado a partir das medições de duas dimensões com o mesmo instrumento e de uma dimensão com outro instrumento. Há, portanto, a combinação de duas grandezas dependentes entre si e de uma terceira delas independente.


Numa situação genérica, deve ser possível calcular a incerteza combinada a partir de uma relação matemática entre grandezas, dos resultados das medições e de parâmetros estatísticos que identifiquem as relações de dependência. Isso é proporcionado pela fórmula a seguir.

#A.1#

Onde:

• g: grandeza resultante das medições x_i, ou seja, g = f( x₁, x₂, ... )
• u(g): incerteza combinada de g
• u(x_i): incerteza da medição da grandeza x_i
• r(x_j, x_k): coeficiente de correlação entre x_j e x_k (algumas informações sobre correlação podem ser vistas na página Probabilidades e estatística V-00 deste site).

Se todas as grandezas são independentes, r(x_j, x_k) = 0, e a parcela do duplo somatório da igualdade #A.1# é nula. Assim, ela se reduz à formula dada em página anterior para grandezas independentes.

Também pode ser notado que a a incerteza aumenta se ocorre dependência, fato já mencionado em páginas anteriores.

Caso particular

Sejam g = f(x₁, x₂, x₃) e os coeficientes de correlação:

r(x₁, x₂) = 1

r(x₁, x₃) = r(x₂, x₃) = 0

Isso significa que as grandezas x₁ e x₂ são dependentes e x₃ é independente. Para esse caso, a fórmula anterior fica reduzida a

#B.1#

Exemplo 01 (Fonte - Concurso Inmetro 2001): Para a determinação do volume de uma peça de aço na forma de um paralelepípedo retângulo, foram utilizados: um micrômetro, para a medição da altura e da largura da seção transversal, e um paquímetro, para a medição do comprimento da seção transversal.

Os valores obtidos para cada uma dessas dimensões foram:

altura: 20,000 ± 0,005 mm

largura: 25,000 ± 0,005 mm

comprimento: 100,00 ± 0,03 mm

Considerando os resultados das medições, é correto afirmar que a incerteza combinada do(a)

(a) área da seção transversal é igual a √ 256,25 mm².

(b) volume total do prisma é igual a 7,5 × 10⁻⁷ mm³.

(c) volume total do prisma é igual a √ 481,25 mm³.

(d) volume total do prisma é igual a √ 731,25 mm³.

(e) volume total do prisma é igual a 37,5 mm³.

Solução: este problema é o caso particular anterior com as seguintes correspondências:

g = f(x₁, x₂, x₃) = x₁ x₂ x₃

₁ = 20,000 u(x₁) = 0,005

x

₂ = 25,000 u(x₂) = 0,005

x

₃ = 100,00 u(x₃) = 0,03

x

As derivadas parciais são:

∂ f / ∂ x₁ = x₂ x₃

∂ f / ∂ x₂ = x₁ x₃

∂ f / ∂ x₃ = x₁ x₂

Substituindo esses valores em #B.1# e dividindo tudo por x₁ x₂ x₃, a igualdade é simplificada para:

[ u(g) / (x₁ x₂ x₃) ]² = [ u(x₁)/x₁ + u(x₂)/x₂ ]² + [ u(x₃)/x₃ ]²

O volume é g = x₁ x₂ x₃ = 20,000 25,000 100,00 = 50000 mm²

Inserindo os valores na igualdade anterior,

[ u(g) / 50000 ]² = [ 0,005/20,000 + 0,005/25,000 ]² + [ 0,03/100,00 ]²

[ u(g) / 50000 ]² = [ 0,00025 + 0,0002 ]² + [ 0,0003 ]² = 29,25 10⁻⁸

u(g) = 5 10⁴ √29,25 10⁻⁴ = √(25 29,25) = √731,25

Resposta (d).

Critério de Chauvenet

Quando se realiza uma seqüência de n medições de um mesmo objeto, é possível a ocorrência de alguns resultados estranhamente fora da distribuição estatística esperada. Em geral, tais resultados podem ser atribuídos a falhas que provocam distorções significativas (exemplo: na medição de tensão elétrica em um ponto de um circuito, a ponta de prova toca acidentalmente em outra parte, alterando o valor).

Os resultados anômalos podem afetar sensivelmente a média e comprometer a exatidão do processo. É razoável, portanto, algum critério para seu descarte. Mas isso não deve ser visto como regra geral. Resultados inesperados às vezes podem ser decisivos no estudo de certos fenômenos.

O critério de Chauvenet é um dos métodos mais simples e mais usados para indicar os resultados a desprezar.

Seja uma seqüência de n medições que estatisticamente seguem o comportamento comum da distribuição normal. Então pode-se rejeitar resultados cujas probabilidades sejam menores que

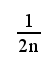#A.1#

Isso significa que resultados considerados "bons" estão dentro de uma faixa cuja probabilidade é

#A.2#

Considerando a curva teórica de uma distribuição normal de média μ e desvio padrão σ conforme Figura 01, pode-se concluir, conforme já visto na página anterior, que esses resultados bons ocupam a faixa central escura, de área igual a [ 1 − 1/(2n) ] × 100%  da área total sob a curva. Naturalmente, os dados a rejeitar ocupam as áreas extremas sob a curva de acordo com indicação da figura.

Fig 01

Pode ser também visto na mencionada página e em outras desta série que as faixas de probabilidades são dadas em termos de desvio-padrão. Assim, para cada valor de n pode ser calculada a probabilidade conforme #A.2# e, por integração matemática da função de densidade da distribuição normal, determinado um coeficiente C correspondente ao número de desvios-padrão para a faixa de valores considerados aceitáveis.

Tab 01
n	C
3	1,38
4	1,54
5	1,65
6	1,73
7	1,80
8	1,87
9	1,91
10	1,96
15	2,13
20	2,24
25	2,33
50	2,57
100	2,81
300	3,14
500	3,29
1000	3,48

A tabela 01 acima dá os valores de C para alguns valores de n. Portanto, a faixa de valores aceitáveis é dada por:

média ± C σ #B.1#

Valores fora dessa faixa podem ser descartados segundo o critério de Chauvenet.

Exemplo numérico

A tabela 02 dá os resultados de uma série hipotética de n = 10 medidas da massa de um determinado corpo.

Tab 02
Medida	Valor
01	2,41
02	2,42
03	2,43
04	2,43
05	2,44
06	2,44
07	2,45
08	2,46
09	2,47
10	4,85

Calculam-se a média e o desvio padrão da amostra segundo fórmulas estatísticas:


Média:

Desvio padrão:

Para n = 10, o coeficiente do critério de Chauvenet é C = 1,96 (Tabela 01).


Multiplicando pelo desvio-padrão,

C s = 1,96 × 0,76 ≈ 1,49

Portanto, os valores confiáveis devem estar entre

2,68 - 1,49 = 1,19  e  2,68 + 1,49 = 4,17

Segundo o critério, pode-se rejeitar a medida 10 (4,85).

Fonte: http://www.mspc.eng.br/tecdiv/med200.shtml